Important Questions of Electricity Class 10 Science Chapter 12

Important Questions of Electricity Class 10 Science Chapter 12

1.  A cylindrical conductor of length ‘l’ and uniform area of cross section ‘A’ has resistance ‘R’. The area of cross section of another conductor of same material and same resistance but of length ‘2l’ is (2020)

(a) A2
(b) 3A2
(c) 2A
(d) 3A
Answer:
(c) : The resistance of a conductor of length!, and area of cross section, A is
R = ρlA
where ρ is the resistivity of the material.
Now for the conductor of length 21, area of cross-section A’ and resistivity ρ.
R’ = ρl′A′ = ρ2lA′
But given, R = R’ ⇒ ρlA = ρ2lA or A’ = 2A

2.  Calculate the resistance of a metal wire of length 2m and area of cross section 1.55 × 106 m², if the resistivity of the metal be 2.8 × 10-8 Ωm. (Board Term I, 2013)
Answer:
For the given metal wire,
length, l = 2 m
area of cross-section, A = 1.55 × 10-6 m²
resistivity of the metal, p = 2.8 × 10-8 Ω m
Since, resistance, R = ρlA
So R = (2.8×10−8×21.55×10−6)Ω
= 5.61.55 × 10-2 Ω = 3.6 × 10-2Ω or R = 0.036Ω

3. Calculate the resistivity of the material of a wire of length 1 m, radius 0.01 cm and resistance 20 ohms. (Board Term I, 2017)

Answer:
We are given, the length of wire, l = 1 m, radius of wire, r = 0.01 cm = 1 × 10-4 m and resistance, R = 20Ω As we know,
R = ρlA, where ρ is resistivity of the material of the wire.
∴ 20Ω.= ρlπr2 = ρ1 m3.14×(10−4)2 m2
∴ ρ = 6.28 × 10-7 Ω m

4. A copper wire has diameter 0.5 mm and resistivity 1.6 × 10-8 Ω m. Calculate the length of this wire to make it resistance 100 Ω. How much does the resistance change if the diameter is doubled without changing its length? (Board Term I, 2015)

Answer:
Given; resistivity of copper = 1.6 × 10-8 Ω m, diameter of wire, d = 0.5 mm and resistance of wire, R = 100 Ω
Radius of wire, r = d2 = 0.52 mm
= 0.25 mm = 2.5 × 10-4 m
Area of cross-section of wire, A = nr²
∴ A = 3.14 × (2.5 × 10-4)²
= 1.9625 × 10-7 m²
= 1.9 × 10-7 m²
As, R = ρlA
∴ 100 Ω = 1.6×10−8Ωm×l1.9×10−7 m2
l = 1200 m
If diameter is doubled (d’ = 2d), then the area of cross-section of wire will become
A’ = πr² = π(d′2)² = π(2d2)² = 4A
Now R ∝ 1A, so the resistance will decrease by four times or new resistance will be
R’ = R4 = 1004 = 25Ω

5. The resistance of a wire of 0.01 cm radius is 10 Ω. If the resistivity of the material of the wire is 50 × 10-8 ohm meter, find the length of the wire. (Board Term I, 2014)

Answer:
Here, r = 0.01 cm = 10-4 m, ρ = 50 × 10-8 Ω m and R = 10 Ω
As, R = ρlA
or l = RAρ=Rρ(πr2)
so l = 1050×10−83.14×(10−4)2
= 0.628 m = 62.8 cm

6. A wire has a resistance of 16 Ω. It is melted and drawn into a wire of half its original length. Calculate the resistance of the new wire. What is the percentage change in its resistance? (Board Term I, 2013)

Answer:
When wire is melted, its volume remains same, so,
V’ = V or A’l’ = Al
Here, l’ = l2
Therefore, A’ = 2 A
Resistance, R = ρlA = 16 Ω
Now, R’ = ρl′A′=ρ(l/2)2A=14ρlA
So, R’ = R4 = 164 = 4 Ω
Percentage change in resistance,
= (R−R′R)×100=(16−416) × 100 = 75%

7. (a) A 6 Ω resistance wire is doubled on itself. Calculate the new resistance of the wire.

(b) Three 2 Ω resistors A, B and C are connected in such a way that the total resistance of the combination is 3 Ω. Show the arrangement of the three resistors and justify your answer. (2020)
Answer:
(a) Given resistance of wire, R = 6 Ω
Let l be the length of the wire and A be its area of
cross-section. Then
R = ρlA = 6 Ω
Now when the length is doubled, l’ = 2l and A’ = A2
∴ R’ = ρ(2l)A/2=4ρlA = 4 × 6 Ω = 24 Ω

(b) Given the total resistance of the combination = 3 Ω
In order to get a total resistance of 3 Ω, the three resistors has to be connected as shown.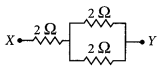

Such that, 1RP=12+12 = 1
⇒ Rp = 1 Ω
and Rs = 2 Ω + 1 Ω = 3 Ω

8. Draw a schematic diagram of a circuit consisting of a battery of 3 cells of 2 V each, a combination of three resistors of 10 Ω, 20 Ω and 30 Ω connected in parallel, a plug key and an ammeter, all connected in series. Use this circuit to find the value of the following :

(a) Current through each resistor
(b) Total current in the circuit
(c) Total effective resistance of the circuit. (2020)
Answer:
The circuit diagram is as shown below.

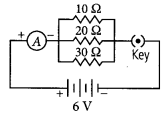
(a) Given, voltage of the battery = 2V + 2V + 2V = 6 V
Current through 10 Ω resistance,
I10 = VR=610 = 0.6 A
Current through 20 Ω resistance,
I20 = VR=620 = 0.3 A
Current through 30 Ω resistance,
I30 = VR=630 = 0.2 A
(b) Total current in the circuit, 1= I10 + I20 + I30
= 0.6 + 0.3 + 0.2 = 1.1 A
(c) Total resistance of the circuit,

1RP=110+120+130=1160



(a) Derive an expression to find the equivalent resistance of three resistors connected in series. Also draw the schematic diagram of the circuit.
(b) Find the equivalent resistance of the following circuit.

Answer:
(a) Refer to answer 37.
(b) For the given circuit,
R1 = 6 Ω, R2 = 10 Ω, R3 = 15 Ω.
As 1Req=1R1+1R2+1R3
1Req=16+110+115
= 5+3+230=1030=13
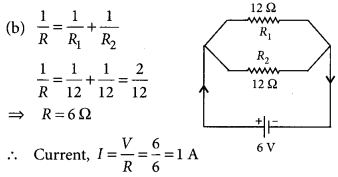
Req = 3 Ω(a) Derive an expression to find the equivalent resistance of three resistors connected in series. Also draw the schematic diagram of the circuit.(b) Find the equivalent resistance of the following circuit.

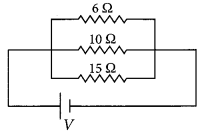
Answer:
(a) Refer to answer 37.
(b) For the given circuit,
R1 = 6 Ω, R2 = 10 Ω, R3 = 15 Ω.
As 1Req=1R1+1R2+1R3
1Req=16+110+115
= 5+3+230=1030=13
Req = 3 Ω

c) Total resistance of the circuit,
1RP=110+120+130=1160

Question 9

(a) With the help of a suitable circuit diagram prove that the reciprocal of the equivalent resistance of a group of resistances joined in parallel is equal to the sum of the reciprocals of the individual resistances.

(b) In an electric circuit two resistors of 12 Ω each are joined in parallel to a 6 V battery. Find the current drawn from the battery. (Delhi 2019)

Answer:

(a) Resistors in parallel : When resistors are connected in parallel.

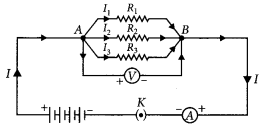
(i) The potential difference across their ends is the same.
(ii) The sum of current through them is the current drawn from the source of energy or cell.
I = I1 + I1 + I3 or VRP=VR1+VR2+VR3
(iii) The equivalent resistance is given by,
1RP=1R1+1R2+1R3
Hence equivalent resistance in parallel combination is equal to the sum of reciprocals of the individual resistances.

10. The resistance of a resistor is reduced to half of its initial value. In doing so, if other parameters of the circuit remain unchanged, the heating effects in the resistor will become

(a) two times       (b) half
(c) one-fourth
(d) four times (2020)
Answer:
(a) : We know, H = I²Rt = V24. t
Now when, R’ = R24, V’ = V and t’ = t
H’ = V′2t′R′=V2tR/2=2V2tR = 2H